Longevity is today one of the main risks assumed by insurance companies and one of the more complex to predict.
In fact, all past predictions have underestimated longevity risk. Predicting how long an individual is going to live depends on several factors, from lifestyle and genetics to environment and medical advances, as even simple ones can significantly influence life expectancies.
Some are even saying that in the future, aging might be treated as a disease condition rather than an inevitability.
Have humans reached the upper lifespan limit? Is 122 years, 164 days – attained two decades ago by Jeanne Louise Calment, the world’s oldest known individual to date – the upper age limit for humans? Or, perhaps, has the person already been born who might live to age 150 or more?
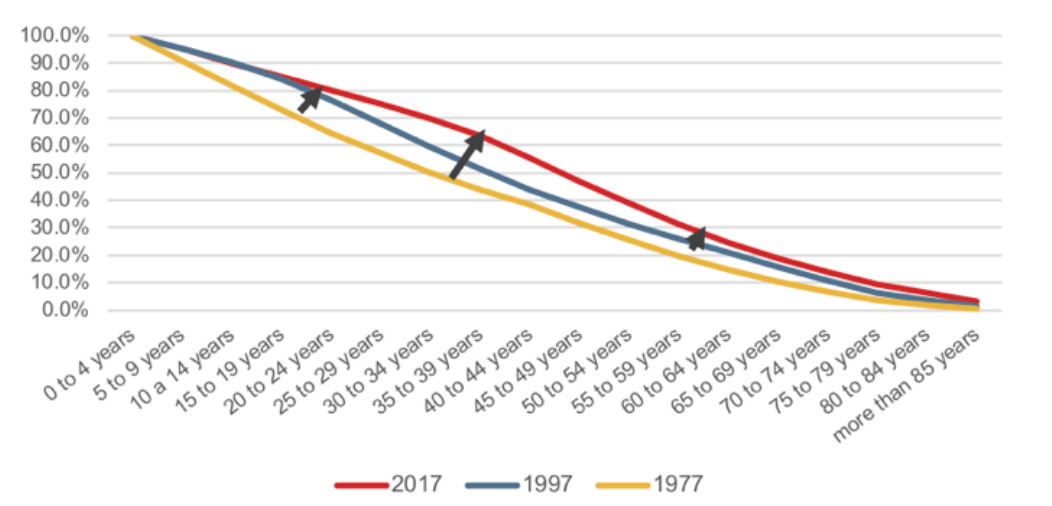
These questions will surely be answered in the future. Today, however, we can confirm the alteration in the shape of the survival curve, called ”squaring” (or “rectangularizing”), which means that no one has yet surpassed Mme. Calment, but more are reaching age 100 and the number of the world’s supercentenarians – people living past their 110th birthdays – is rising fast.
Figure 1 shows the survival curve squaring in Spain from 1977 to 2017, and shows the percentage of survivors for each age band, using Instituto Nacional de Estadistica (Spanish Statistical Office) data.
Figure 1:
Survivors by age band in Spain
 Source: Spanish Statistical Office
Source: Spanish Statistical Office
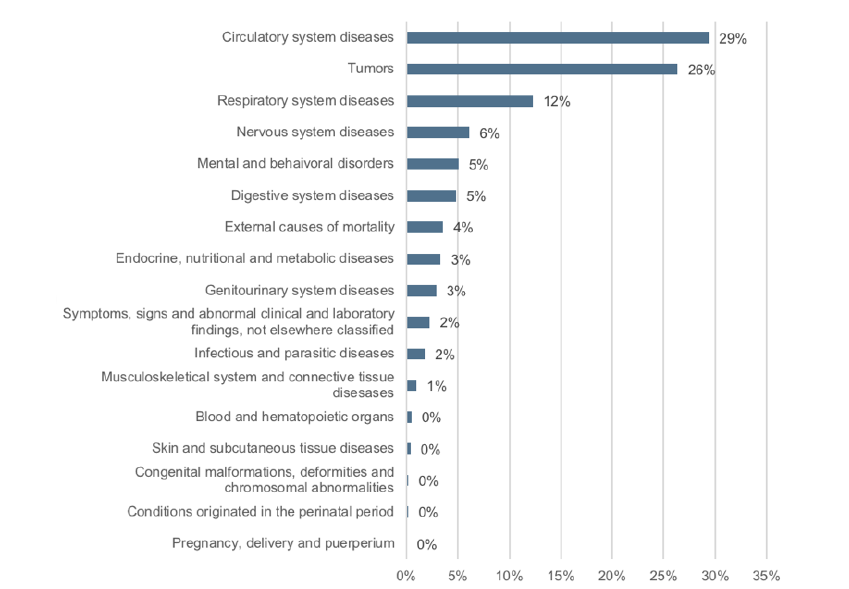
Main causes of death in Spain
Figure 2 depicts the main causes of death in Spain in 2015. The three most frequent causes –circulatory system conditions, cancerous tumors, and respiratory diseases – caused approximately 70% of mortality that year.
Figure 2:
Main mortality drivers in Spain
Source: Spanish Statistical Office
If a cure for cancer were to be found, mortality rates due to cancer would surely decline, yielding a modified distribution of causes of death. Life expectancies of newborns would also increase.(Life expectancy in Spain is already age 83 as of 2016, up from age 79 in 1996.) Might a cure also make it possible for people to age beyond 122 years 164 days? Perhaps, but right now any increase in longevity is unlikely to be significant, which would continue to favor the survival curve squaring.
Can longevity risk be estimated?
For a better understanding of longevity risk, it may be broken down into three sub-risks:
- Base risk: the probability there will be an increase or decrease in the death or disability rates because average mortality or morbidity risk assessments are incorrect.
- Trend risk: the uncertainty about long-term trends (generally calculated using past trends).
- Volatility risk: a measure of the randomness in the mortality or morbidity claim amounts in the near future.
Risk mitigation and data processing
Actuaries have a range of tools and techniques to mitigate these risks.
- For base risk, for example, more data can improve results.
- For trend risk, assess the impact of qualitative changes such as medical advances or lifestyle alterations.
- For volatility risk, ensure adequate portfolio diversification and underwriting risk selection, and use advanced statistical modeling and analysis techniques for valuation.
From a statistical and modeling point of view, it is imperative to collect good historical data to calculate mortality improvement factors. Mortality is not static: it is dynamic and behaves differently in different generations. Using a static mortality table (broken down by age) as an assessment tool can be improved materially by using generational tables, which have a base death rate table and incorporate improvement factors that differ by age, generation and calendar year.
Finally, the data must clearly indicate whether it comes from the general population or the insured population. Each has different behaviors, and population data can be risky to use to project estimates in insured populations. Therefore, selection adjustments are made.
Measurement and valuation
There is no one ideal predictive model. There are many advanced models today that allow us to estimate longevity risk more accurately, and each one adjusts to different realities.
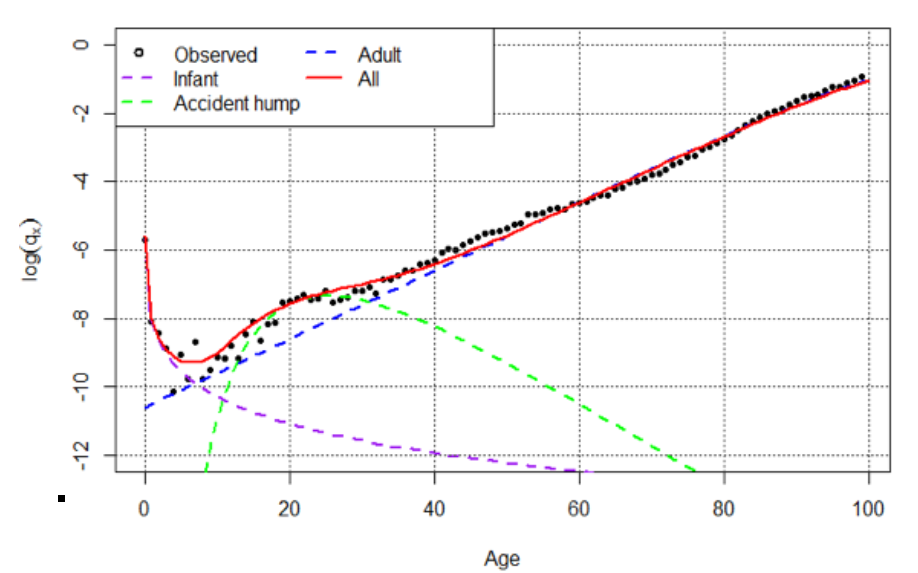
Figure 3 shows three factors involved in the probability of death at different ages:
- Child mortality;
- Accidents at young ages; and,
- Mortality due to disease in more mature ages
Figure 3:
FACTORS INVOLVED IN THE PROBABILITY OF DEATH AT DIFFERENT AGES
 Source: RGASource: RGA, Human Mortality Database
Source: RGASource: RGA, Human Mortality Database
Today there are advanced models that allow us to estimate longevity risk with more accuracy. In particular, among others we can highlight the best known: Lee-Carter, P-splines, Whittaker-Henderson, Renshaw-Haberman, and even specific models for advanced ages where there is very little data, such as Kannistö. As an example, the Lee Carter model fits the Spanish reality for ages over 45, but for older ages, it is no longer reliable.
Which one to use? It depends on the portfolio that one wants to project into the future. Each model suits a particular need; however, the model to use should be simple model to apply.
How to manage longevity risk from a risk and economic capital point of view?
Risk management is not the same as the economic capital management.
- Risk management is a structured approach to identifying, analyzing, measuring and responding to all possible risk factors, in such a way that the fluctuation relative to a threat can be managed.
- Economic capital is the unexpected maximum loss in a determined future period (in Solvency II, 12 months) and a given confidence level (in Solvency II, 99.5%). This means that the greater the risk assumed, the more economic capital is needed. Economic capital measures risk using economic realities rather than accounting and regulatory rules, and is thought to give a more realistic representation of a firm's solvency.
Risk itself is not a negative, but it must be managed. One way to do so is by managing economic capital, which measures what would happen in an adverse scenario of remote risk. The European solvency framework (Solvency II) establishes a volume of minimum own funds to cover this remote scenario.
Solvency II’s longevity shock figure of 20% for the risk is high. Indeed, this onerous economic capital requirement may be harming annuity sales. The shock requires insurers to allocate more assets to Own Funds to mitigate the impact of having policies in their portfolios for individuals with longer life expectancies than initially expected. The required valuation of the longevity shock, as can be seen in Figures 4 and 5, is a single, immediate and permanent reduction of 20% of expected mortality. This would be approximately equivalent to eradicating more than 65% of deaths due to circulatory causes, or reducing cancer mortality by 70% in Spain.
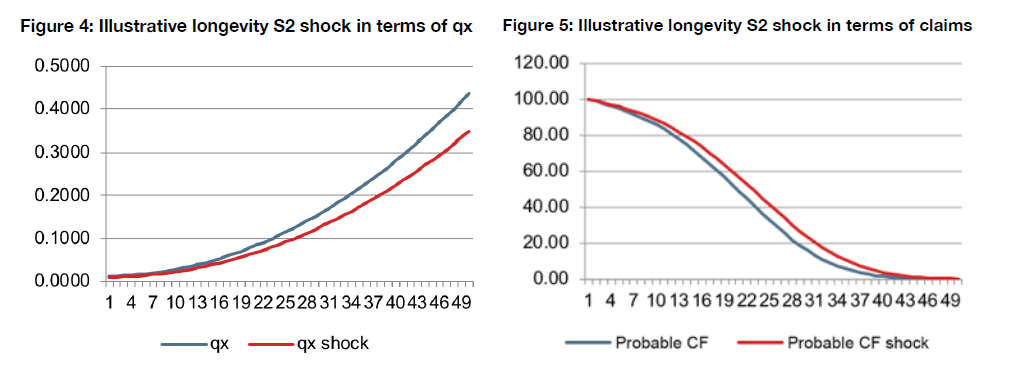 Source: GRM95
Source: GRM95
Solutions for managing risk and economic capital are not the same.
The question insurers need to ask in relation to their annuity portfolios and the decision on the solution is: what is the source of the concerns? Should longevity-driven capital requirements be reduced, or should 100% of future longevity exposure be covered? It is not the same to cover all longevity risk or cover only a remote risk. The optimal solution may differ.
Reinsurance as a tool to mitigate longevity risk
Many solutions have emerged to cover and manage longevity risk, such as a natural cover subscribing mortality risk that can offset the potential impact (e.g., a life annuity with a death benefit). However, an efficient solution can be to transfer the risk to a third party, such as a reinsurer.
Reinsurance-based solutions can manage longevity risk and economic capital. Next, we will describe two potential solutions for the management of longevity risk and for the management of economic capital derived from longevity.
1. Reinsurance solution for risk management, or high-risk transfer.
In this type of reinsurance, known as an indemnity longevity swap, the direct company cedes all or part of its total longevity risk. This alternative would have the same impact on the longevity Solvency Capital Requirement (SCR) as would a capital optimization solution. However, the price is much higher than that of a low-risk transfer (explained below), given that the reinsurer, in exchange for fixed payments in the future, assumes the total annuity benefit payments in case of a negative mortality deviation (i.e., insured lives in the portfolio die later than expected).
The basic idea is to make a swap between future uncertain annuity payments and certain pre-established future premiums, and to do so in such a way that reinsurance can cover future losses, according to the agreed-upon quota share of the risk, if there is an unfavorable deviation in the longevity assumptions.
Figure 6:
ILLUSTRATING CASH FLOW PAYMENT UNDER AN INDEMNITY LONGEVITY SWAP

Source: RGA
2. Reinsurance solution for economic capital management, or low-risk transfer.
This strategy, known as a longevity shock absorber or longevity index-based hedges, enables the transfer of a portion of tail risk within the stress scenario to improve insurer’s capital position. It is a Stop-Loss Cover to reduce capital requirements for biometric risks under the stress scenarios of Solvency II’s standard formula.
In Solvency II, the standard calculation of economic capital assumes a remote risk equivalent to a single, immediate and permanent reduction of 20% on the probability of death.
The reinsured benefit is based on a defined range (interval) within the stress scenario defined as between:
- An attachment point (AP) that will not be close to 0% because it is not a remote risk and the associated cost would be very high
- A detachment point (DP), which could be 20% or slightly lower.
This solution might help reduce the Solvency II capital requirement derived from the longevity risk between the AP and the DP. The upside in this type of reinsurance is retained by the ceding company.
The probability of actual death is associated with a known index, and is typically based on a general population and not an insured population, which entails a basis risk that is taken into account in the solution.
The cost of this strategy is materially lower than that of an indemnity longevity swap, since the risk that is reinsured is not the whole future annuity benefit payment. The reinsured benefit is defined as the interval [AP, DP] within the interval [0%, 20%] of the longevity Solvency II stress scenario.
This solution only transfers remote longevity risk, but this remote risk has a material impact on the capital requirements of Solvency II. Own Funds globally are reduced, although in turn, this decrease is greatly mitigated by the reduction in the risk margin thanks to the reinsurance solution.
Figure 7 illustrates the impact of the shock absorber solution before and after reinsurance. The total capital consumption is being reduced from €148 mill to €81 mill, mainly due to the drop of the longevity capital requirement. The recoverable amount of reinsurance has a negative effect on Own Funds of €68 million, which is offset by an increase in Own Funds of €50 million due to the reduction of the risk margin.
Figure 7:
Impact on Solvency II capital requirements and own funds
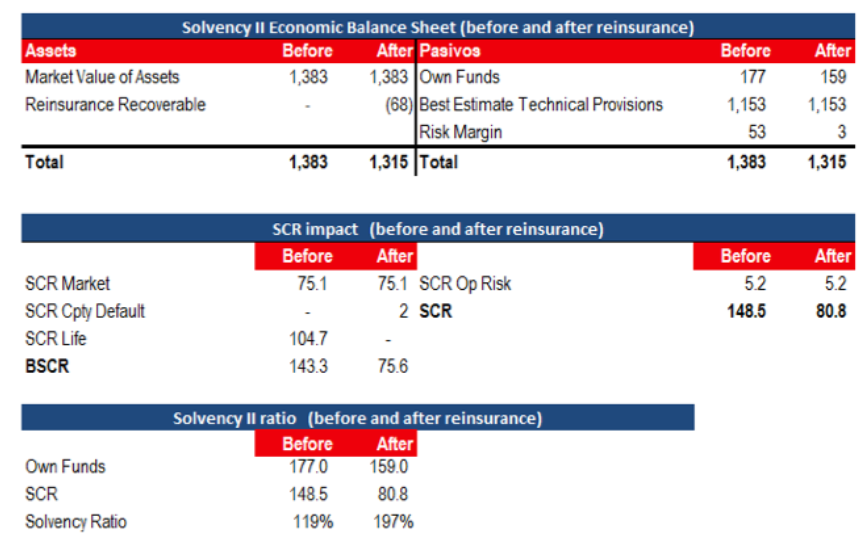
Source: RGA
Note: it has been assumed that in life insurance there are only life and whole of life annuity portfolios. For illustrative purposes, we wanted to exaggerate the impact by assuming an AP of 0% and a DP of 20%.
Cost of these longevity solutions
These solutions do come with a cost; but it should be taken into account that the reinsurer is assuming a long-term risk with a high level of uncertainty. In addition, these solutions assume the cost of economic capital is burdensome to the ceding company.
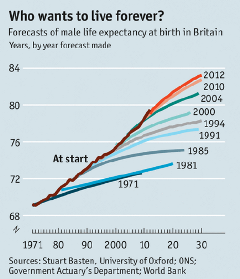
It is assumed by the life insurance industry that longevity reinsurance solutions are probably not cheap. However, if we analyze the graph to the left which corresponds to the different predictions about the life expectancy of a male newborn in the United Kingdom since 1971, we observe that the longevity estimates that have been made in the past have always been short with respect to reality (brown line)
SOURCES: THE ECONOMIST; STUART BASTEN, UNIVERSITY OF OXFORD; ONS; GOVERNMENT ACTUARY’S DEPARTMENT; WORLD BANK
Conclusion
Despite being faced with one of the most complicated challenges for insurance companies, given the long timeframes involved, the insurance industry should be able to provide a solution to a social need, and be able to offer products designed to meet retirement needs at a reasonable price given long-term risk. Reinsurance through the use of current models and techniques, together with adequate risk management tools and use of economic capital can help to provide this solution.



 Source: Spanish Statistical Office
Source: Spanish Statistical Office
 Source: RGASource: RGA, Human Mortality Database
Source: RGASource: RGA, Human Mortality Database Source: GRM95
Source: GRM95